Questions regarding how the Klippel NFS works are raised in many of Amir's speaker reviews. Thomas has suggested starting a thread on this topics and here I am. I am starting this thread with a brief description of the basic principles behind the NFS. You can find much further details on the theory in the DIY 3D speaker scanner thread.
What the Klippel NFS systems does is to approximate the speaker under test into the sum of a number of spherical wave expansion functions (source):

These spherical wave expansion functions are solutions to the Helmholtz equation. They describe the propagation of the sound waves at a single frequency ω. If we know the coefficients C_mn, we can simply plug in the coordinates r, θ, and φ into this equation, and we can obtain the sound pressure magnitude (and phase) p at any point in space for frequency ω. The numbers will be the same as those measured with a microphone at same location inside an anechoic chamber.
The spherical harmonics Y_mn(θ, φ) in these functions define the angular directivity (θ is the vertical/polar angle, φ is the horizontal/azimuthal angle). The radial/distance (r) dependency is defined by the Hankel functions. The cutoff order of the spherical harmonics N will determine the number of terms in the summation, which is equal to (N+1)^2. The more complex the speaker geometry and/or the higher the frequency is, the larger N is needed to give an accurate approximation.
Conceptually, what these spherical wave expansion functions do is to mathematically transform a speaker into a sound radiating sphere. Picture a spherical surface that entirely encloses the speaker. All sound radiated from the speaker will have to travel through this spherical surface to reach the outside. If we can produce a sound source in the shape of a ball that has the exact sound radiating pattern as on that spherical surface, then this ball shaped sound source can perfectly replicate or replace the speaker, and a listener (or microphone) on the outside will not be able to tell any difference.
The NFS system measures at a number of points around the speaker. The coefficients (C_mn) are determined using the measured data. For every measurement point, we know p, ω, r, θ and φ. (We also know k, which is called the acoustic wave number, and it is equal to ω divided by the speed of sound.) For a chosen N, we have to solve for (N+1)^2 coefficients. The Klippel NFS measures at more than (N+1)^2 points and uses linear regression to calculate the coefficients C_mn and estimate the errors. The process is for a single frequency, and it needs to be replicated for every frequency of interest (e.g. 20 - 20 kHz at X frequencies per octave).
Once we have obtained the coefficients, we can use the equation and plug-in new coordinates to predict the sound pressures anywhere in space. Reconstructions are not limited to the far field. They are also valid for near field (but with limitations which I will not get into in this post).
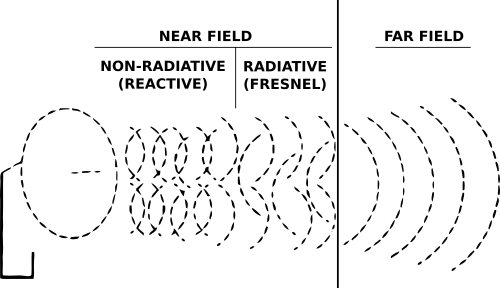
Some may be aware of discussions about the measurement axis. For the NFS, since we approximate the sound source as a sphere, we want the center of this sphere (expansion center) to be close to the actual acoustic center of the speaker, which is the center point of the driver generating the sound. Since sound wave radiations are much more complex at high frequencies, matching the two is far more important for high frequencies. The expansion center is unrelated to the listening axis, as the equation allows us to reconstruct at any arbitrary points in 3D space. We can point the listening axis to anywhere we desire, and adjust our reconstruction points coordinates accordingly.
This concludes this first post. Further discussions are welcomed.
[Edit:] Post #10 gives an explanation of sound field separation (the method of extracting anechoic data from measurements made in a normal reflective room).
What the Klippel NFS systems does is to approximate the speaker under test into the sum of a number of spherical wave expansion functions (source):
These spherical wave expansion functions are solutions to the Helmholtz equation. They describe the propagation of the sound waves at a single frequency ω. If we know the coefficients C_mn, we can simply plug in the coordinates r, θ, and φ into this equation, and we can obtain the sound pressure magnitude (and phase) p at any point in space for frequency ω. The numbers will be the same as those measured with a microphone at same location inside an anechoic chamber.
The spherical harmonics Y_mn(θ, φ) in these functions define the angular directivity (θ is the vertical/polar angle, φ is the horizontal/azimuthal angle). The radial/distance (r) dependency is defined by the Hankel functions. The cutoff order of the spherical harmonics N will determine the number of terms in the summation, which is equal to (N+1)^2. The more complex the speaker geometry and/or the higher the frequency is, the larger N is needed to give an accurate approximation.
Conceptually, what these spherical wave expansion functions do is to mathematically transform a speaker into a sound radiating sphere. Picture a spherical surface that entirely encloses the speaker. All sound radiated from the speaker will have to travel through this spherical surface to reach the outside. If we can produce a sound source in the shape of a ball that has the exact sound radiating pattern as on that spherical surface, then this ball shaped sound source can perfectly replicate or replace the speaker, and a listener (or microphone) on the outside will not be able to tell any difference.
The NFS system measures at a number of points around the speaker. The coefficients (C_mn) are determined using the measured data. For every measurement point, we know p, ω, r, θ and φ. (We also know k, which is called the acoustic wave number, and it is equal to ω divided by the speed of sound.) For a chosen N, we have to solve for (N+1)^2 coefficients. The Klippel NFS measures at more than (N+1)^2 points and uses linear regression to calculate the coefficients C_mn and estimate the errors. The process is for a single frequency, and it needs to be replicated for every frequency of interest (e.g. 20 - 20 kHz at X frequencies per octave).
Once we have obtained the coefficients, we can use the equation and plug-in new coordinates to predict the sound pressures anywhere in space. Reconstructions are not limited to the far field. They are also valid for near field (but with limitations which I will not get into in this post).
Some may be aware of discussions about the measurement axis. For the NFS, since we approximate the sound source as a sphere, we want the center of this sphere (expansion center) to be close to the actual acoustic center of the speaker, which is the center point of the driver generating the sound. Since sound wave radiations are much more complex at high frequencies, matching the two is far more important for high frequencies. The expansion center is unrelated to the listening axis, as the equation allows us to reconstruct at any arbitrary points in 3D space. We can point the listening axis to anywhere we desire, and adjust our reconstruction points coordinates accordingly.
This concludes this first post. Further discussions are welcomed.
[Edit:] Post #10 gives an explanation of sound field separation (the method of extracting anechoic data from measurements made in a normal reflective room).
Last edited:

 Ideally at two positions along the x-axis.
Ideally at two positions along the x-axis.