Does that mean we do not need our speaker to produce square waves because our signal does not go past 24kHz? Then what would be a good standard to follow? For example if we feed square wave signal, what would be the ideal outcome for speaker?1.
IMO it is misleading to create such squarewaves as they clearly hurt the Nyquist-Shannon sampling theorem.
A squarewave consists of its base sinewave plus odd sinewaves 3rd, 5th, 7th, 11th ... order, see also https://en.wikipedia.org/wiki/Square_wave
Now at e.g. 48 kHz samplewrate the top frequency is 24 kHz. So there is no squarewave above 8 kHz, only sinewaves, because the max. frequency is limiting the harmonics.
So the Audacity squarewave is not a true bandlimited squarewave, indeed it creates many aliasing frequencies.
2.
A squarewave can be considered as a step into positive direction followed by a step into negative direction. The steps are repeating and the step times define the frequency of the squarewave.
Now if the step response of a speaker is known the response on a squarewave excitation can already be estimated quite well.
Indeed you can also convolve the pulse measurement of the speaker with the squarewave.
With a typical passive speaker with step response tweeter first, then midrange driver and finally bass driver you will get a squarewave response as expected.
3.
Usually a speaker does not transfer very low frequencies, it has a high-pass behaviour. By this reason the resulting "squarewaves" show a falling top and a rising bottom.
Summary: it is quite 'dangerous' to stick with the ideal picture of a squarewave, taken from the analog world. The result in the "sampling" domain is heavily influenced by the Nyquist criteria. Furthermore the highpass behaviour of the speaker changes the shape of the squarewave. So with low frequency squarewaves the top/bottom show up tilted. At higher frequencies this gets hidden by zooming into picture. Here the limitation of the bandwidth creates the typical oscillations on top/bottom. Finally the resulting squarewave is deformed by the characteristics of the speaker pulse response which can already be seen by the step response display calculated from the pulse response.
-
WANTED: Happy members who like to discuss audio and other topics related to our interest. Desire to learn and share knowledge of science required. There are many reviews of audio hardware and expert members to help answer your questions. Click here to have your audio equipment measured for free!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Time Domain measurements?
- Thread starter 73hadd
- Start date
- Joined
- Apr 29, 2020
- Messages
- 169
- Likes
- 131
It answers with it’s transfer function. That is amplitude over frequency and phase over frequency. Actually you can use a variety of stimuli. I use a log sine sweep because it is the most robust against intruding noise because it has the highes crest factor. Being at it I can also measure harmonic distortion at the same time with the Farina method. Actually I do a double sweep also when I use the Transfer Function Module of my KLIPPEL. Distortion can then be seen separated in negative time before the impulse response.
- Joined
- Apr 29, 2020
- Messages
- 169
- Likes
- 131
When you use a digital system, say a DA converter on top of that you see the time response of the converter. That comes from the various anti aliasing filers.
- Joined
- Jul 10, 2019
- Messages
- 124
- Likes
- 338
And if you measure your system with microphone and soundcard also keep in mind that the analog-digital conversion also limits the frequency range by brickwall filters (against aliasing) and samplerate (max. frequency is fs/2).When you use a digital system, say a DA converter on top of that you see the time response of the converter. That comes from the various anti aliasing filers.
So there are many good reasons why a squarewave measurement does not look like an ideal squarewave.
haraldo
Active Member
And if you measure your system with microphone and soundcard also keep in mind that the analog-digital conversion also limits the frequency range by brickwall filters (against aliasing) and samplerate (max. frequency is fs/2).
So there are many good reasons why a squarewave measurement does not look like an ideal squarewave.
Doesn't that point to the fact that there are severe phase issues?
As far as I understand the brickwall filters will create significant phase issues, in which case the square wave points to phase issues resulting from the brick wall filter. Am I fully on the wrong planet here?
I mean, what is the point of having perfect handling of phase/time in the digital domain when we need a filter at the end that mess up everything?
Doesn't that point to the fact that there are severe phase issues?
There are no severe phase issues in the typical electronics.
As far as I understand the brickwall filters will create significant phase issues, in which case the square wave points to phase issues resulting from the brick wall filter. Am I fully on the wrong planet here?
There are no severe phase issues in the typical electronics.
A square wave is a construct - not a natural thing.
A frequency (sine wave) with an amplitude + 3x the frequency at 1/3 the amplitude + 5x the frequency at 1/5th the amplitude on out to infinity.
Am I fully on the wrong planet here?
You're on the only known habitable planet.
I mean, what is the point of having perfect handling of phase/time in the digital domain when we need a filter at the end that mess up everything?
It doesn't "mess up everything".
- Joined
- Jul 10, 2019
- Messages
- 124
- Likes
- 338
Some examples of a truly bandlimited squarewave @48 kHz samplerate:
100 Hz
1500 Hz
7500 Hz
The last example consists of 2 frequencies only - 7500 Hz and 22500 Hz. The next higher frequency of order 5 would be 37500 Hz but this is already outside of the bandwidth limit 24 kHz.
100 Hz
1500 Hz
7500 Hz
The last example consists of 2 frequencies only - 7500 Hz and 22500 Hz. The next higher frequency of order 5 would be 37500 Hz but this is already outside of the bandwidth limit 24 kHz.
KaiserSoze
Addicted to Fun and Learning
- Joined
- Jun 8, 2020
- Messages
- 699
- Likes
- 592
Does that mean we do not need our speaker to produce square waves because our signal does not go past 24kHz? Then what would be a good standard to follow? For example if we feed square wave signal, what would be the ideal outcome for speaker?
Yes, we do not need for our speaker to produce squares, for that reason and for other reasons. It think it is useful to identify three reasons, two of which are not controversial. With respect to the 3rd reason there is good consensus here and throughout most of the audio community, however there are plenty of people who remain skeptical or on the fence.
Reason #1: A square wave transitions instantaneously between two different levels, which is to say, it contains a vertical slope. The steepest slope in a waveform determines the highest frequency component needed to represent the waveform in an equivalent Fourier series of pure sinusoids. Which is to say that there is a direct correspondence between steepness and frequency. Since frequencies higher than a threshold (generally taken to be 20 kHz) are not audible, there is no need for an amplifier or especially a speaker to reproduce the vertical slopes seen in a square wave. When a square wave is passed through an audio device, the vertical slopes are replaced with slopes that obviously are not vertical. In fact the upper frequency limit of the device may be inferred from the steepness of the slope in the output. The act of suppressing frequencies above a threshold is also evident in a ripple that overlays the output waveform; the replacement of the vertical slope with a non-vertical slope may be thought of as an aspect of the ripple.
Reason #2: If the fundamental frequency of the square wave is below the lowest frequency the audio device is capable of reproducing, the output will look similar to the input, but the fundamental frequency of the square wave will be missing. Because of the other odd-order, low-order frequency components it will still somewhat resemble the original square wave, but not nearly the same as when the fundamental frequency of the square wave is well within the passband of the audio component. If we accept that we cannot hear below a certain threshold, generally accepted to be 20 Hz, then there is no need for an audio device to preserve the fundamental frequency of a square wave if the fundamental frequency of the square wave is below this threshold.
Reason #3: If the numerous and various frequency components needed to produce a square wave (subject to the two preceding considerations) are not phase-coherent, then the output will not look anything like a square wave. It will have the required frequency components, but if the different frequency components vary appreciably in phase they will also vary appreciably in time. There is a long history associated with the question of whether it matters. There was a period about a half-century ago when many people simply assumed that this mattered, and when it was vogue to demonstrate the ability of a loudspeaker to emulate an amplifier in preserving the general appearance of a square wave. Nowadays the prevailing view is that human ear cannot hear the difference, which view is justifiable given the apparent lack of evidence to the contrary in spite of any number of experiments designed to demonstrate that we are able to hear the difference.
If you accept the prevailing view on this question, then it follows that square waves are worse than worthless when it comes to assessing audio equipment. One other type of waveform that similarly reveals the extent of preservation of phase and time coherency remains in use, and while it is closely related to the square wave, it is used for a limited purpose and is interpreted accordingly, the expectation being that it will yield information about correct phase alignment of the two drivers in the overlap region of the crossover. But there are questions about whether even this is legitimate, because correct phase alignment does not assume that the two drivers are aligned in phase or in time. It assumes that the offset in phase and in time between the two drivers is consistent throughout the overlap region, such that the amount of destructive interference and phase cancellation that occurs between the two acoustic waveforms will be constant throughout the overlap.
KaiserSoze
Addicted to Fun and Learning
- Joined
- Jun 8, 2020
- Messages
- 699
- Likes
- 592
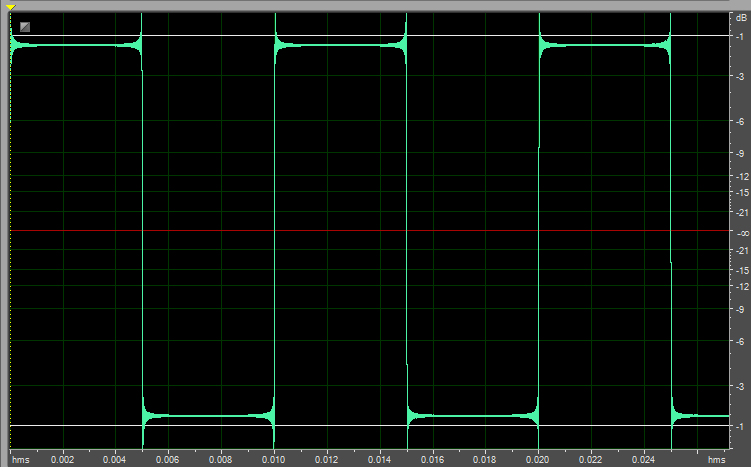
Some examples of a truly bandlimited squarewave @48 kHz samplerate:
100 Hz
View attachment 73112
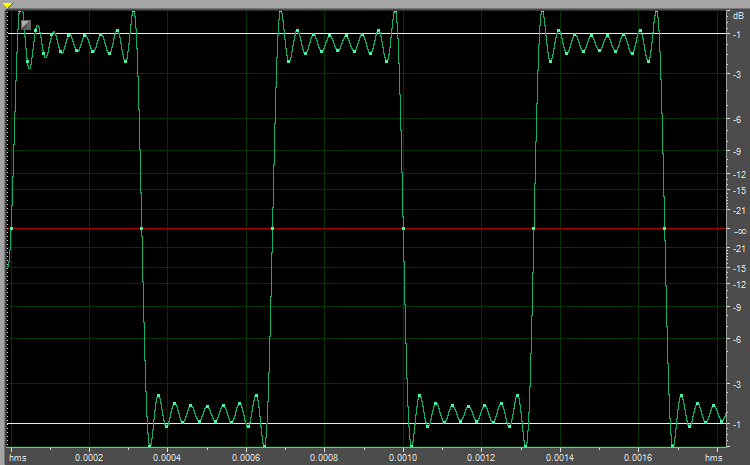
1500 Hz
View attachment 73113
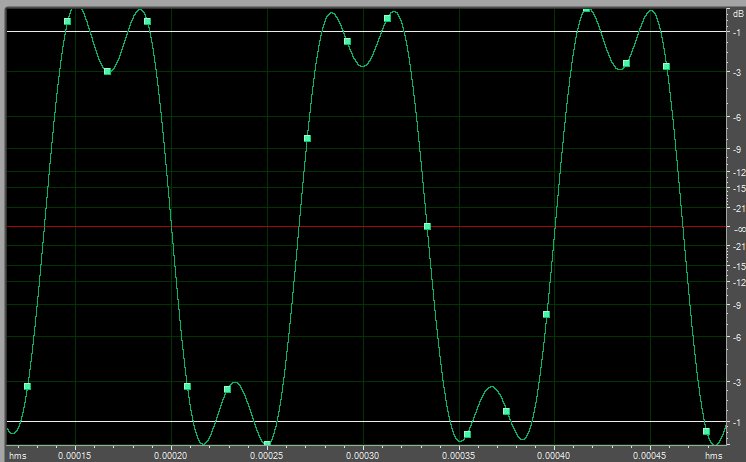
7500 Hz
View attachment 73114
The last example consists of 2 frequencies only - 7500 Hz and 22500 Hz. The next higher frequency of order 5 would be 37500 Hz but this is already outside of the bandwidth limit 24 kHz.
Very nice. A picture is worth a thousand words, someone once said. Worth noting is the fact that the first example looks more like a square wave because, since the fundamental is lower in frequency, 100 Hz vs. 1.5 kHz and 7.5 kHz, a great many more of its harmonics are within the audible spectrum and are included. The sides of it appear to be nearly vertical, but if the horizontal scaling were stretched it would be apparent that the steepness of the sides (the rate of change) is determined by the highest harmonic that is included.
What "might" happen when you send a 200Hz square to the speakers, if you have a sub and a two-way:
(repaired image)
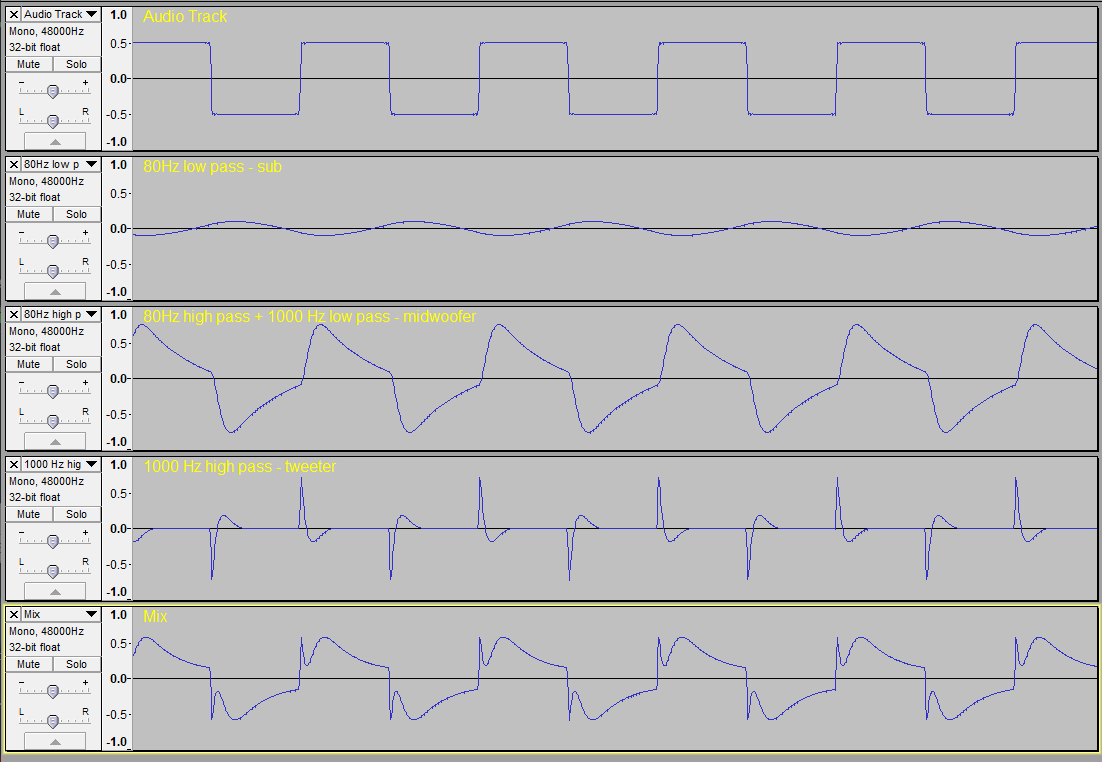
(repaired image)
Last edited:
KaiserSoze
Addicted to Fun and Learning
- Joined
- Jun 8, 2020
- Messages
- 699
- Likes
- 592
What "might" happen when you send a 200Hz square to the speakers, if you have a sub and a two-way:
View attachment 73138
Hmmm. The waveform you show for the subwoofer contains some very high-frequency components as evidenced by the steep vertical rise. If the low-pass 80 Hz filter applied to it is brick-wall, the sub won't even produce the fundamental for a 200 Hz sine wave. With a real filter that isn't brick wall you will see an attenuated 200 Hz sine wave, modulated very slightly by a 600 Hz, etc. But there isn't any way that any subwoofer is going to output a waveform with steep sides like you show. I haven't closely studied the other two outputs you show, but I expect there are similar issues.
I used 12dB/octave.
Just an amateur's experimental observation.
Or maybe I screwed up.
Will correct the post.
Thank you.
Just an amateur's experimental observation.
Or maybe I screwed up.
Will correct the post.
Thank you.
- Joined
- Jul 10, 2019
- Messages
- 124
- Likes
- 338
Here is my result with 200 Hz squarewave and 80 Hz lowpass 12 dB/octaveI used 12dB/octave.
Just an amateur's experimental observation.
Or maybe I screwed up.
Will correct the post.
Thank you.
Yes. My mistake.
I thought it looked odd, too.
I thought it looked odd, too.
- Joined
- May 8, 2020
- Messages
- 642
- Likes
- 658
Not quite, brickwall filters are known as linear-phase filters. They actually preserve the phase of the original signal or try to preserve the signal as much as possible.Doesn't that point to the fact that there are severe phase issues?
Example of AcourateDRC's effect on a square wave signal sent to my speakers:
Original digital signal sent to the system
Preamp output without DRC - 25 foot noisy cable to PC sound card for capture
Preamp output with DRC for MartinLogan speakers with subs
Preamp output with DRC for JBL LSR 308
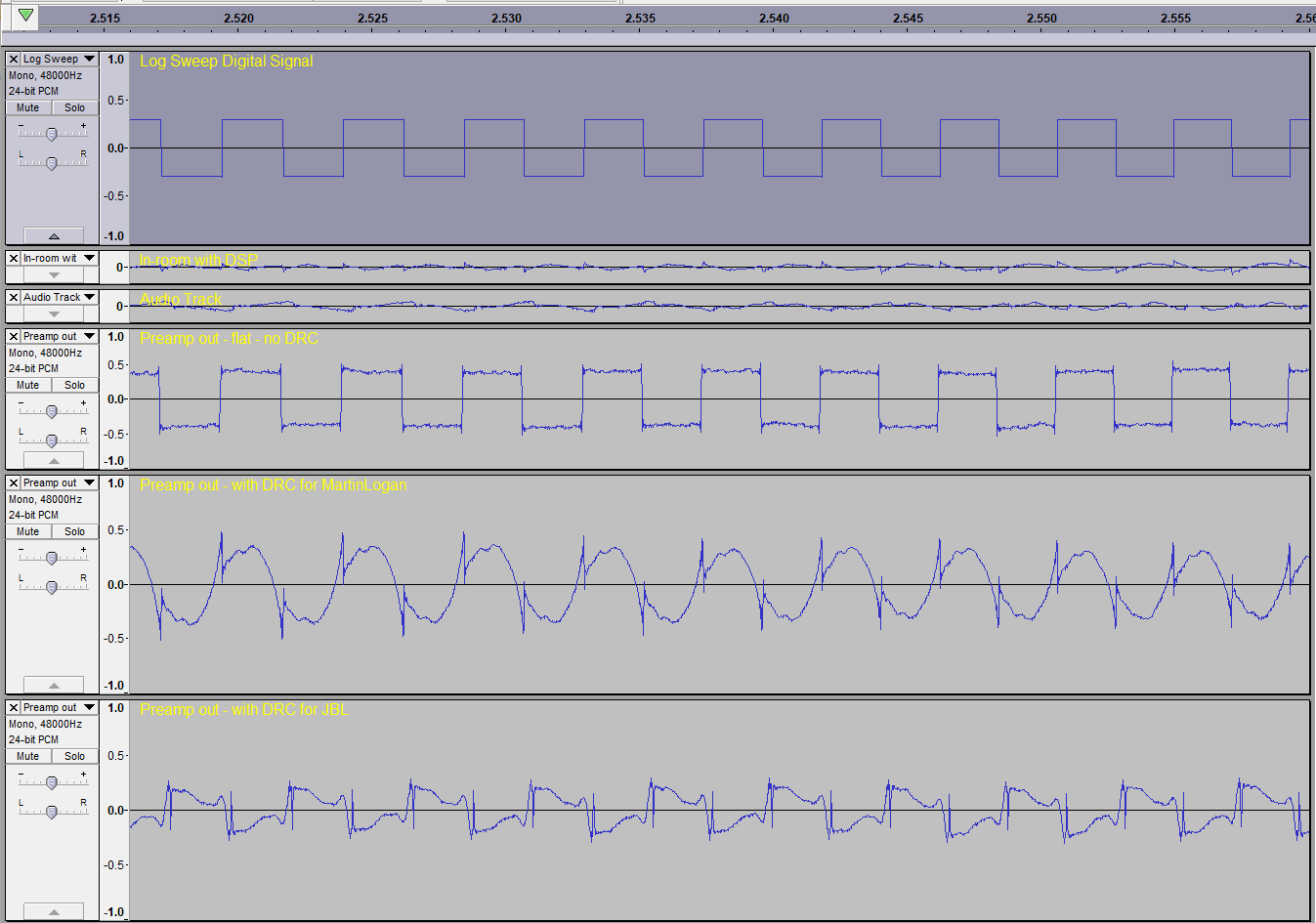
Original digital signal sent to the system
Preamp output without DRC - 25 foot noisy cable to PC sound card for capture
Preamp output with DRC for MartinLogan speakers with subs
Preamp output with DRC for JBL LSR 308
KaiserSoze
Addicted to Fun and Learning
- Joined
- Jun 8, 2020
- Messages
- 699
- Likes
- 592
Yes, we do not need for our speaker to produce squares, for that reason and for other reasons. It think it is useful to identify three reasons, two of which are not controversial. With respect to the 3rd reason there is good consensus here and throughout most of the audio community, however there are plenty of people who remain skeptical or on the fence.
Reason #1: A square wave transitions instantaneously between two different levels, which is to say, it contains a vertical slope. The steepest slope in a waveform determines the highest frequency component needed to represent the waveform in an equivalent Fourier series of pure sinusoids. Which is to say that there is a direct correspondence between steepness and frequency. Since frequencies higher than a threshold (generally taken to be 20 kHz) are not audible, there is no need for an amplifier or especially a speaker to reproduce the vertical slopes seen in a square wave. When a square wave is passed through an audio device, the vertical slopes are replaced with slopes that obviously are not vertical. In fact the upper frequency limit of the device may be inferred from the steepness of the slope in the output. The act of suppressing frequencies above a threshold is also evident in a ripple that overlays the output waveform; the replacement of the vertical slope with a non-vertical slope may be thought of as an aspect of the ripple.
Reason #2: If the fundamental frequency of the square wave is below the lowest frequency the audio device is capable of reproducing, the output will look similar to the input, but the fundamental frequency of the square wave will be missing. Because of the other odd-order, low-order frequency components it will still somewhat resemble the original square wave, but not nearly the same as when the fundamental frequency of the square wave is well within the passband of the audio component. If we accept that we cannot hear below a certain threshold, generally accepted to be 20 Hz, then there is no need for an audio device to preserve the fundamental frequency of a square wave if the fundamental frequency of the square wave is below this threshold.
Reason #3: If the numerous and various frequency components needed to produce a square wave (subject to the two preceding considerations) are not phase-coherent, then the output will not look anything like a square wave. It will have the required frequency components, but if the different frequency components vary appreciably in phase they will also vary appreciably in time. There is a long history associated with the question of whether it matters. There was a period about a half-century ago when many people simply assumed that this mattered, and when it was vogue to demonstrate the ability of a loudspeaker to emulate an amplifier in preserving the general appearance of a square wave. Nowadays the prevailing view is that human ear cannot hear the difference, which view is justifiable given the apparent lack of evidence to the contrary in spite of any number of experiments designed to demonstrate that we are able to hear the difference.
If you accept the prevailing view on this question, then it follows that square waves are worse than worthless when it comes to assessing audio equipment. One other type of waveform that similarly reveals the extent of preservation of phase and time coherency remains in use, and while it is closely related to the square wave, it is used for a limited purpose and is interpreted accordingly, the expectation being that it will yield information about correct phase alignment of the two drivers in the overlap region of the crossover. But there are questions about whether even this is legitimate, because correct phase alignment does not assume that the two drivers are aligned in phase or in time. It assumes that the offset in phase and in time between the two drivers is consistent throughout the overlap region, such that the amount of destructive interference and phase cancellation that occurs between the two acoustic waveforms will be constant throughout the overlap.
Sometimes I have to make an adjustment to something I wrote even when no one else cares.
With respect to a square wave with fundamental frequency below 20 Hz, the question is how the square wave will be transformed when processed by a piece of audio gear that filters frequencies below 20 Hz. To answer this, let us suppose that the fundamental frequency of a square wave is 15 Hz and that a "brick wall" filter is in place at around 20 Hz. If this filter is truly a brick wall as it were, then the 3rd harmonic at 45 Hz will pass through with no attenuation, whereas the 15 Hz fundamental will be fully attenuated. The output will contain no evidence of the original 15 Hz fundamental. It will somewhat resemble a square wave, but one where the fundamental frequency is the 45 Hz 3rd harmonic of the original square wave.
- Joined
- May 8, 2020
- Messages
- 642
- Likes
- 658
No, that filter you are describing is a notch filter or a high-pass filter. Brickwalls are low-pass filters, which if you place it around 20 Hz, anything above that frequency will be filtered. High-pass filters are the ones that filter frequencies below a cutoff.that a "brick wall" filter is in place at around 20 Hz. If this filter is truly a brick wall as it were,
- Joined
- Jul 10, 2019
- Messages
- 124
- Likes
- 338
A 15 Hz square wave consists of sine waves 15 Hz, 45 Hz (3*15), 75 Hz (5*15), 105 Hz (7*15) ...Sometimes I have to make an adjustment to something I wrote even when no one else cares.
With respect to a square wave with fundamental frequency below 20 Hz, the question is how the square wave will be transformed when processed by a piece of audio gear that filters frequencies below 20 Hz. To answer this, let us suppose that the fundamental frequency of a square wave is 15 Hz and that a "brick wall" filter is in place at around 20 Hz. If this filter is truly a brick wall as it were, then the 3rd harmonic at 45 Hz will pass through with no attenuation, whereas the 15 Hz fundamental will be fully attenuated. The output will contain no evidence of the original 15 Hz fundamental. It will somewhat resemble a square wave, but one where the fundamental frequency is the 45 Hz 3rd harmonic of the original square wave.
Now you take away 15 Hz and get a lowest frequency 45 Hz. So far ok.
But 75 Hz is not 3*45, 105 Hz is not 5*45 ... Thus the filtered result is no longer a square wave.
dc655321
Major Contributor
- Joined
- Mar 4, 2018
- Messages
- 1,597
- Likes
- 2,235
No, that filter you are describing is a notch filter or a high-pass filter. Brickwalls are low-pass filters, which if you place it around 20 Hz, anything above that frequency will be filtered. High-pass filters are the ones that filter frequencies below a cutoff.
Also, no.
"Brickwall" refers to the slope of a filter's transition band. Rejecting high or low frequencies is irrelevant.
Granted, the phrase is often in the context of lowpass filters...
Similar threads
- Replies
- 13
- Views
- 783
- Replies
- 11
- Views
- 1K
- Replies
- 10
- Views
- 625
- Replies
- 149
- Views
- 28K
- Replies
- 1
- Views
- 427
