Mod note: our technical expert @DonH56 wrote this series article a while back. As I get time, I am porting them here.
Alternating current carriers in a conductor tend to travel near the surface. This happens due to opposing eddy currents from the magnetic field generated whenever alternating current (a.c.) flow is present. These are not generated by direct (d.c.) flow since current flow is all in the same direction and thus opposing eddy currents are not created. The effect is frequency-dependent, resulting in carriers traveling closer to the surface at higher frequencies. Because less cross-sectional conductor area is used as frequency increases, the effective resistance rises as frequency increases. Note that at d.c. (0 Hz) the entire cross-sectional area of the conductor is utilized.
Skin depth (sd) is the depth at which current density has fallen to about 1/3 (actually, 1/e, or about 0.37x) the density at the surface. The definition arises from EM equations beyond the scope of this article. A related term is the penetration depth (T), the depth by which virtually all current in the conductor flows. If the depth is greater than the conductor’s depth, then the conductor’s entire cross-sectional area will be used and d.c. and a.c. resistance will be essentially the same. At higher frequencies, only part of the conductor’s depth may be used, and effective (a.c.) resistance increases.
Figure 1 shows both parameters (skin depth and penetration depth) over frequency, from 10 Hz to 100 kHz, for copper wires. As you can see, by 1 kHz it is around 0.1”, and at 20 kHz the skin depth is only 0.018”, with T = 0.025”. This is for an isolated wire; parallel or coaxial conductors cause a slight (~3%) change.
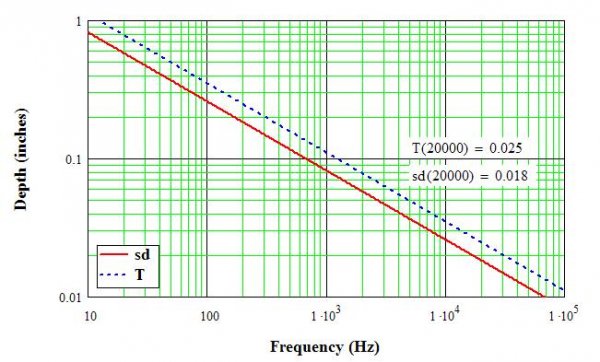
Figure 1: Skin Depth (sd) and Penetration (T) vs.Frequency
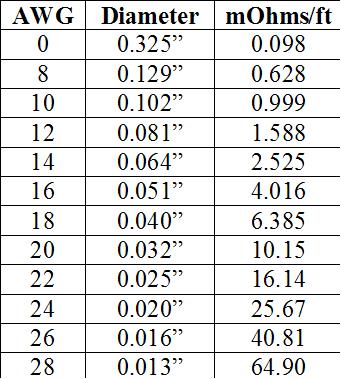
How much this matters in audio circuits is a matter of debate (of course). The table below shows the diameter of various wire gauges commonly used. Note that stranded or solid wire type has little impact on these calculations, though d.c. resistance is just a hair higher for stranded wire. Litz wire, bundles of smaller-diameter insulated wires, can be used to reduce the impact of skin effect. At 20 kHz, all the diameter of 22-gauge wire or smaller is utilized, and a.c. and d.c. resistance are essentially the same. Larger wire will be impacted by skin depth, with only about 31 % the diameter of a 12-gauge wire being utilized to carry signal current. However, note that the d.c. resistance of AWG 12 wire is only about 10 % that of AWG 22, so even after giving up so much due to skin effect, you are still better off than using the smaller wire.
In the real world interconnect impedances are so much higher than wire resistance (for typical cables) that skin depth is a non-issue, IMO. For speaker cables, while there is a clear argument for larger gauges to improve damping factor and provide high current capacity, skin depth is generally not a concern because the cables are larger and higher impedance can usually be tolerated at higher frequencies. Recognize that the d.c. resistance of a 10-foot piece of AWG 12 cable is only 0.016 ohms, still a very small number compared to the impedance of most speakers, so if skin depth doubles or triples that value at 20 kHz it is still a very small fraction of the load impedance, and much smaller than the output impedance of most amplifiers at 20 kHz.
This will not stop the debate, of course.
References:
1. Wikipedia article: http://en.wikipedia.org/wiki/Skin_effect
2. Reference Data for Radio Engineers, 5th ed., Howard W. Sams & Co, 1968
Alternating current carriers in a conductor tend to travel near the surface. This happens due to opposing eddy currents from the magnetic field generated whenever alternating current (a.c.) flow is present. These are not generated by direct (d.c.) flow since current flow is all in the same direction and thus opposing eddy currents are not created. The effect is frequency-dependent, resulting in carriers traveling closer to the surface at higher frequencies. Because less cross-sectional conductor area is used as frequency increases, the effective resistance rises as frequency increases. Note that at d.c. (0 Hz) the entire cross-sectional area of the conductor is utilized.
Skin depth (sd) is the depth at which current density has fallen to about 1/3 (actually, 1/e, or about 0.37x) the density at the surface. The definition arises from EM equations beyond the scope of this article. A related term is the penetration depth (T), the depth by which virtually all current in the conductor flows. If the depth is greater than the conductor’s depth, then the conductor’s entire cross-sectional area will be used and d.c. and a.c. resistance will be essentially the same. At higher frequencies, only part of the conductor’s depth may be used, and effective (a.c.) resistance increases.
Figure 1 shows both parameters (skin depth and penetration depth) over frequency, from 10 Hz to 100 kHz, for copper wires. As you can see, by 1 kHz it is around 0.1”, and at 20 kHz the skin depth is only 0.018”, with T = 0.025”. This is for an isolated wire; parallel or coaxial conductors cause a slight (~3%) change.

Figure 1: Skin Depth (sd) and Penetration (T) vs.Frequency
How much this matters in audio circuits is a matter of debate (of course). The table below shows the diameter of various wire gauges commonly used. Note that stranded or solid wire type has little impact on these calculations, though d.c. resistance is just a hair higher for stranded wire. Litz wire, bundles of smaller-diameter insulated wires, can be used to reduce the impact of skin effect. At 20 kHz, all the diameter of 22-gauge wire or smaller is utilized, and a.c. and d.c. resistance are essentially the same. Larger wire will be impacted by skin depth, with only about 31 % the diameter of a 12-gauge wire being utilized to carry signal current. However, note that the d.c. resistance of AWG 12 wire is only about 10 % that of AWG 22, so even after giving up so much due to skin effect, you are still better off than using the smaller wire.

In the real world interconnect impedances are so much higher than wire resistance (for typical cables) that skin depth is a non-issue, IMO. For speaker cables, while there is a clear argument for larger gauges to improve damping factor and provide high current capacity, skin depth is generally not a concern because the cables are larger and higher impedance can usually be tolerated at higher frequencies. Recognize that the d.c. resistance of a 10-foot piece of AWG 12 cable is only 0.016 ohms, still a very small number compared to the impedance of most speakers, so if skin depth doubles or triples that value at 20 kHz it is still a very small fraction of the load impedance, and much smaller than the output impedance of most amplifiers at 20 kHz.
This will not stop the debate, of course.
References:
1. Wikipedia article: http://en.wikipedia.org/wiki/Skin_effect
2. Reference Data for Radio Engineers, 5th ed., Howard W. Sams & Co, 1968
Last edited by a moderator:


