DDF
Addicted to Fun and Learning
- Joined
- Dec 31, 2018
- Messages
- 617
- Likes
- 1,360
Going down the rabbit hole of room EQ can be overwhelming and confusing, with critical hands-on information dispersed or hard to find. Here's a summary of targets and methods using REW, minimizing the fat and focusing on what's important.
Olive/Toole (e.g. reference):
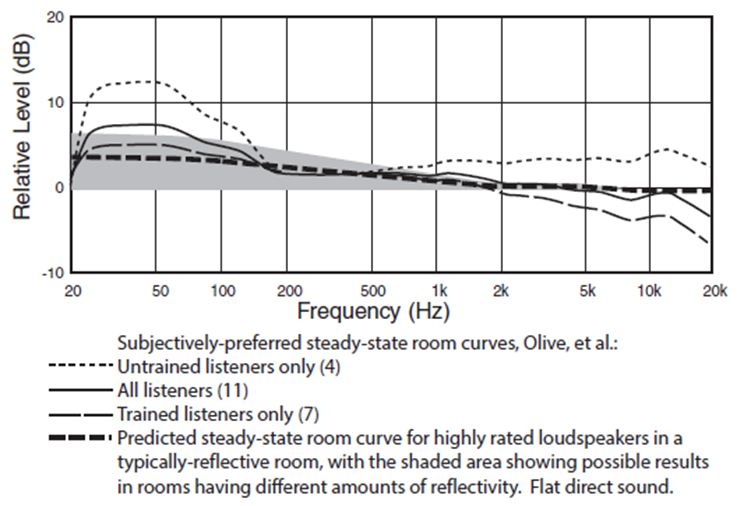
The bass rise preference is explained as human adaptation to the room (expectation). See house target files @ https://mehlau.net/audio/dirac-live-2/
Trained listeners preferred curve: 0dB @ 200Hz, +2dB @ 100Hz, +4dB @ ≤ 50 Hz
Target sound level for preference graph based on levels in ITU-R BS1116:
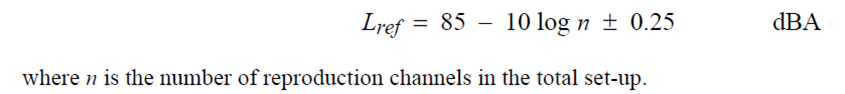
From JJ (Acoustic and Psychoacoustic issues in Room Correction room_correction.ppt):


REW
Special considerations for digital equalization
Olive/Toole (e.g. reference):
- Steady state room curves are not definitive of sound quality above a few hundred Hz
- Equalizing a lesser loudspeaker to match that room curve doesn’t guarantee equivalent sound quality
- Speaker EQ: EQ listening window of the speaker measured anechoic
- Room EQ: EQ room peaks below Schroeder frequency (~ 300 Hz)
- Use spatial averaging. Single point measurements are inadequate (edited on request)
The bass rise preference is explained as human adaptation to the room (expectation). See house target files @ https://mehlau.net/audio/dirac-live-2/
Trained listeners preferred curve: 0dB @ 200Hz, +2dB @ 100Hz, +4dB @ ≤ 50 Hz
Target sound level for preference graph based on levels in ITU-R BS1116:
From JJ (Acoustic and Psychoacoustic issues in Room Correction room_correction.ppt):
- Large peaks should be equalized (especially for first reflections)
- Large, sharp dips are not to be touched, remember the energy storage issue
- Broad dips can be equalized out for a broader listening area
- Don’t eq phase
- Equalize gain and delay from each speaker just for the first arrival, which locks in the spatial cues
- If you equalize only below 500Hz or so, you get a .5 foot radius space, give or take, where the cancellation makes some sense
- Flattening each channel individually … provides the measurably “flattest” response
- Recommends fixing l-r matching as most important “corrects the most obvious defects”
- First reflection cancellation… individual adjustment for each channel
- It removes the “boxy” sound to some extent
- Fixing this for the listening location means that putting more impairments elsewhere in room
- Can be adjusted to avoid obvious impairments and still have some productive effect.
- Can clean up “boom” to some extent as well
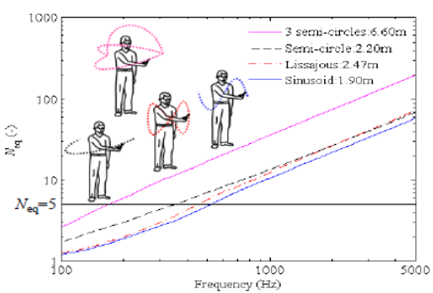
- Ear’s equivalent rectangular bandwidth: BW resolution of ear. Use this for setting the smoothing of the measurement used for EQ.
REW
- Help file: https://www.roomeqwizard.com/REWhelp.pdf
- Sharp dips are non-minimum phase, leave them alone. Peaks are minimum phase, EQ them
- Single point method is too constraining. Use multipoint average or moving mic RTA.
- For room RTA’s with moving mic method:
- Use pink noise or periodic (necessary if using rectangular window) pink noise
- Use RTA mode, not Spectrum, to see room frequency response. Spectrum needs white noise
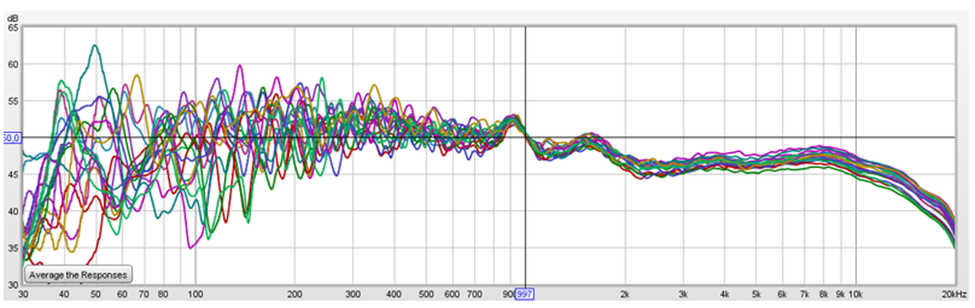
- Recommend Blackmann-Harris window as it provides best discrimination of sharp peaks and dips but slightly worse frequency resolution. Rectangular has the worst leakage. Plot below shows an example of a 1kHz tone from an external generator with a Rectangular window followed by Hann.
- FFT frequency resolution = sample rate/FFT length. As FFT length is increased the analyser starts to overlap its FFTs, calculating a new FFT for every block of input data. The degree of overlap is 50% for 16k, 75% for 32k, 87.5% for 64k and 93.75% for 128k. The overlap ensures that spectral details are not missed when a Window is applied to the data. The maximum overlap allowed can be limited using the Max Overlap control below to reduce processor loading at higher FFT lengths.
- Average “forever” for at least 60 seconds
- Select RTA capture in main window
- In RTA window select “current” to load response for EQ
- To calculate PEQs, “Match response to target” and save using “Save Filter Settings as Text”
- For sweep measurements
- Default sweep length = 256k (÷sample rate = duration (s)). SNR +3dB per double sweep length. To avoid synch issues, use longer sweeps vs averaged sweeps. Note: acoustic timing reference feature can synch multi measurements but doesn’t work with subs
- Measure multiple locations, & average (not vector average, average shouldn’t include phase)
- Only use vector averaging if trying to eq phase. See REW_rePhase_tuto.pdf
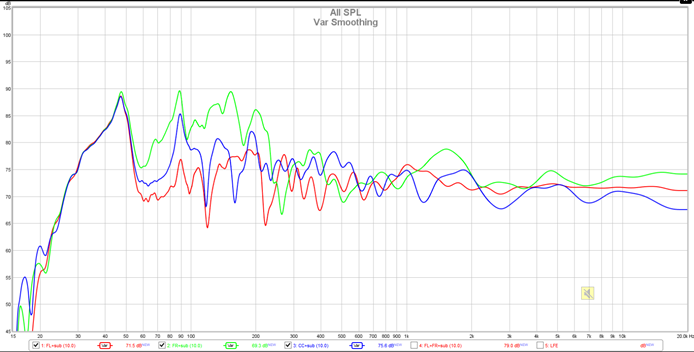
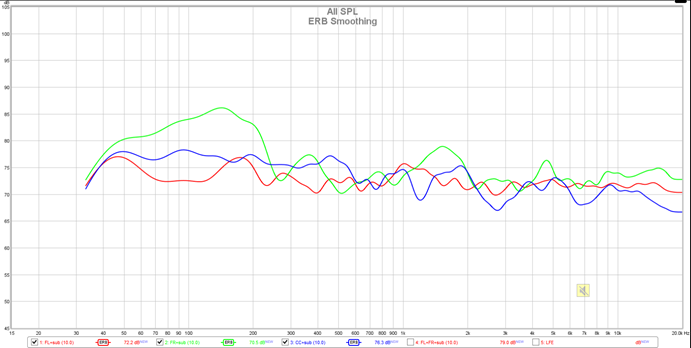
- Variable smoothing applies 1/48 octave below 100 Hz, 1/3 octave above 10 kHz and varies between 1/48 and 1/3 octave from 100 Hz to 10 kHz, reaching 1/6 octave at 1 kHz. Variable smoothing is recommended for responses that are to be equalised.
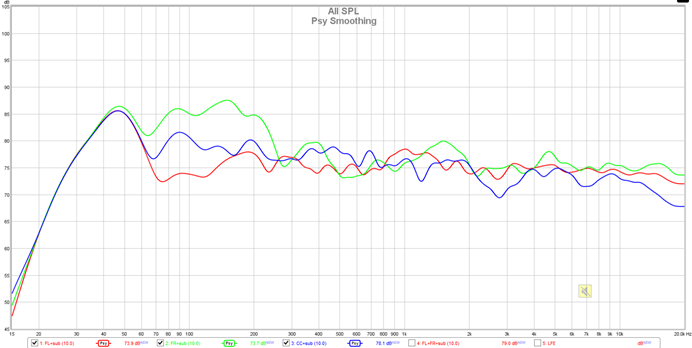
- Psychoacoustic smoothing uses 1/3 octave below 100Hz, 1/6 octave above 1 kHz and varies from 1/3 octave to 1/6 octave between 100 Hz and 1 kHz. It also applies more weighting to peaks by using a cubic mean (cube root of the average of the cubed values) to produce a plot that more closely corresponds to the perceived frequency response.
- ERB smoothing uses a variable smoothing bandwidth that corresponds to the ear's Equivalent Rectangular Bandwidth, which is (107.77f + 24.673) Hz, where f is in kHz. At low frequencies this gives heavy smoothing, about 1 octave at 50Hz, 1/2 octave at 100 Hz, 1/3 octave at 200 Hz then levelling out to approximately 1/6 octave above 1 kHz.
- Smoothing impact examples (examples from ASR post, lost attribution):
- Variable smoothing
- Psychoacoustic Smoothing
- ERB Smoothing
- FFT: frequency dependent window (FDW) can be specified in cycles or in octaves, to capture only limited reflections at mid frequencies while not sacrificing low frequency resolution. If the width is in cycles a 15 cycle window (for example) would have a width of 150 ms at 100 Hz (15 times 10 ms), 15 ms at 1 kHz (15 times 1 ms) and 1.5 ms at 10 kHz (15 times 0.1 ms). It is set in preferences, analysis tab. MLSSA Adaptive window (Room mode) recommends 50ms ≥1 kHz, log_freq-log_ms to 270ms ≤ 70Hz
- https://www.audiosciencereview.com/...stortion-abx-testing.18709/page-2#post-659017 “my personal experience is that correcting to direct sound sounds more neutral to me than correcting to 5-6 cycles FDW above transition frequency”
- House curves
- Format: plain text, frequency followed by space, comma+space or tab
- Only lines starting with a number are loaded
- Harman curves found at https://mehlau.net/audio/dirac-live-2/
- Trained listeners preferred curve: 0dB @ 200Hz, +2dB @ 100Hz, +4dB @ ≤ 50 Hz
- REW eq target: 2dB/oct 200Hz to 50 Hz
- Adaptive windows (like MLSSA or REW’s FDW) can’t be relied on alone
- Use RTA and pink noise (equal energy per octave so 3 dB/oct & 10dB/decade slope in a log plot)
- Mic needs to be calibrated for random incidence diffuse field
- Move the mic (include vertical) and average over the entire time record (not sliding average)
- Average at least 60 seconds for < 100Hz. Average the squared sound pressure (not with phase). Eg, use RTA average “forever” in REW
- Don’t point at loudspeaker, keep @ 90 degree incidence
- The distance travelled for the average affects accuracy
- Scan over at least 5 meters (big circles) for acceptable error. 10 m is better
- Keep mic no closer than 1m to boundaries
- Move 1 meter per 3 seconds max speed
- This is same method as used for the Sonos
- Aim for +/- 2dB accuracy (1/6 octave smoothed)
- https://www.ohl.to/:
- Hereunder are 9 MMM measurements of the same loudspeaker (Behringer B2030A, with both LF, HF switches at -2 and -4dB) in 9 different rooms (10 to 30 m2 surfaces) at distances between 2 and 3m. It clearly shows that :
- under 300Hz, the room is the key
- between 300 and 800Hz, the room and the loudspeaker are both important
- above 800Hz, the loudspeaker is the main factor. The response is the same but the slope depends of the distance and the room absorption
- Hereunder are 9 MMM measurements of the same loudspeaker (Behringer B2030A, with both LF, HF switches at -2 and -4dB) in 9 different rooms (10 to 30 m2 surfaces) at distances between 2 and 3m. It clearly shows that :
Special considerations for digital equalization
- Simple high pass filtering can change the waveform envelope and increase peak values compared to unfiltered: https://science-of-sound.net/2016/08/sh-html/
- Its not known how great this peaking can be in practice, and how much margin needs to be created. From study of on-line sources, 4 dB should be enough for music
- Taking a total systems design approach, I found and verified through set up and test that it's often very advantageous to create excess overlap between the subwoofer and main speakers. The biggest advantages are:
- Through the overlap frequencies you get the same benefit as multiple subs where a plurality of sources can reduce the room mode peaks and dips
- it causes a bass peak due where they overlap which increases system gain in a very useful range. Equalization is then used in both the sub and main amplifier channels to compensate. This has two significant benefits:
- it reduces the amplifier power needed in that range
- more importantly, it reduces the displacement required from the woofers in the main speaker woofers, lowering distortion. It's like getting some to much of the benefits of a high pass crossover on the mains, without needing one. I have two systems set up this way and it works great, verified via REW and the grin-meter
- Care needs to be taken to ensure the sub isn’t localizable, if its too loud compared to the mains
- When manually adjusting, this calculator determines Q for a given bandwidth
- Equalizer APO
- When implementing filters in EAPO, REW "generic filter produces same filter settings as used by EAPO (so "cramping" matches)
- RBJ Audio EQ cookbook equations suffer from cramping at high frequencies due to their dependency on the bi-linear transform.
- https://sourceforge.net/p/equalizerapo/discussion/general/thread/e2fd040bcc/#4561/4773
- “Spanish Harlem” from Rebecca Pidgeon’s The Raven has a very nice acoustic bass in the key of G that uses the classic 1, 4, 5 progression. The bass fundamental frequencies that go with the progression:
- 49 62 73 65 82 98 73 93 110 Hz
- Look for even levels of all notes
- Recommends eqing phase as it improves depth and makes sound a bit less bright, though its subtle
- Recommends using programs that don’t use MMM, claims MMM over-corrects because it averages. Also argues to non fill dips, as they’re non minimum phase
Attachments
Last edited:

