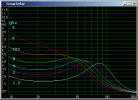
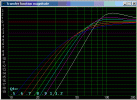
For phase p and frequency f group delay GD is the negative of the derivative of the change in phase with respect to the change in frequency: GD = -dp/df. In general phase is a function of frequency p(f); that is, phase changes with frequency. That's the math behind it.
A change in phase is equivalent to a time shift, for example a 180-degree phase shift is like shifting the time by one-half cycle of the signal. The derivative is a fancy expression for the slope of a line, so it is a measure of phase linearity. A straight (linear) line has the form y = mx+b where every point x is multiplied by the slope m and added to offset b to produce a y value. For a straight line, m is constant (just a number, not a function of something else), and hopefully we remember this formula from school. Now replace m with GD so to get a straight line, that means the change in phase divided by the change in frequency must be constant, meaning group delay is a constant, and every frequency is delayed by the same amount of time. What goes in, comes out again, exactly as it was but just a little later in time.
Now, a pulse, or musical signal, includes many frequencies. If we send the signal through a component like an amplifier or speaker with constant group delay, then every frequency is delayed the same amount, and the output is just like the input except delayed in time. If the group delay is not constant, that means different frequencies have different delays through the component, so at the other end the signal will be "smeared" in time with different frequencies arriving at different times. Things like transient attacks from drums or instruments will not be as clean. There are various studies discussing just how far off the delay can be at different frequencies before we notice it, some referenced in the Wikipedia article mentioned previously (https://en.wikipedia.org/wiki/Group_delay_and_phase_delay).
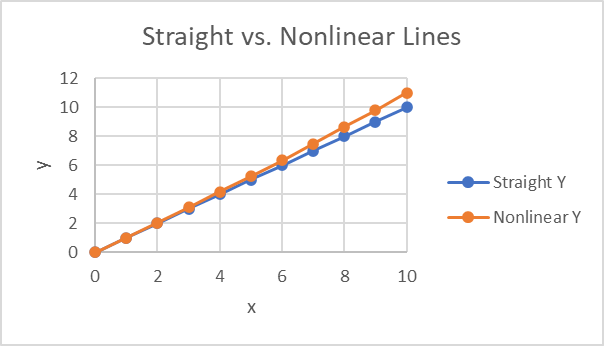
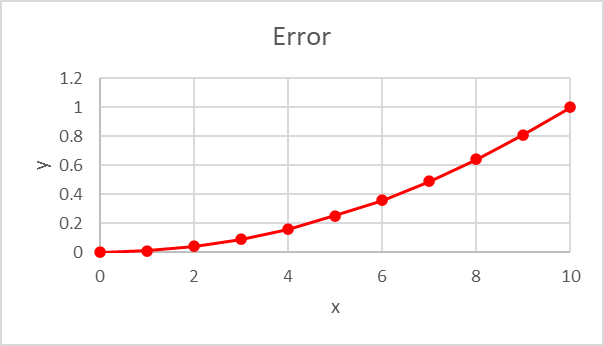
A straight line of y = mx with m = 1 looks like the blue line below. If I make the slope (m) depend upon the input (x) we get the orange line, which is no longer perfectly straight. The next plot shows the error. This is what happens when group delay is not constant, the (phase) line is no longer straight.
Now try with some signals, in this case the first five frequencies in a square wave. The amplitudes decrease as frequency goes up and only odd harmonics are used (see https://www.audiosciencereview.com/.../composition-of-a-square-wave-important.1921/). Notice how all nine signals line up in the middle and again at the end.
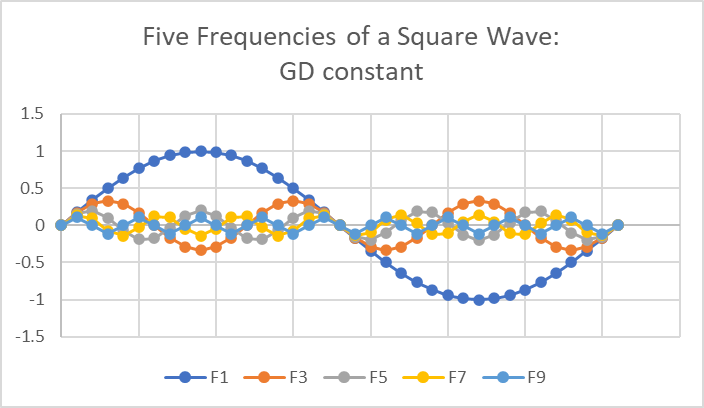
If all the signals arrive at the same time, that is group delay is constant, then this is what you see when you add them all up:
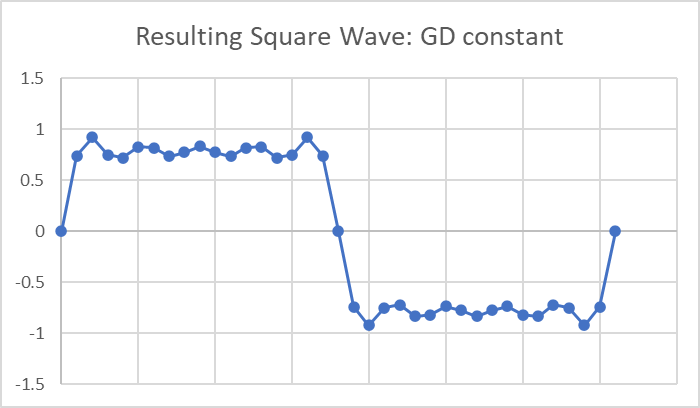
A perfect square wave has frequencies out to infinity, and this is just five, so it does not have perfectly sharp (straight) edges and the top and bottom are not perfectly flat. It is perfectly symmetric, however, with edges and top and bottom the same across the entire period.
Now adjust the group delay so it is not constant but instead each successively higher frequency is shifted just a little bit more. Notice how the signals no longer align perfectly in the middle and at the end but are spread out a bit:
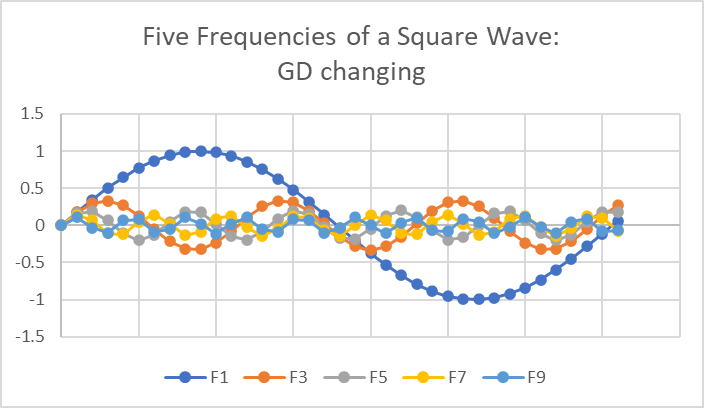
The output when we sum them all looks different and is no longer symmetric:
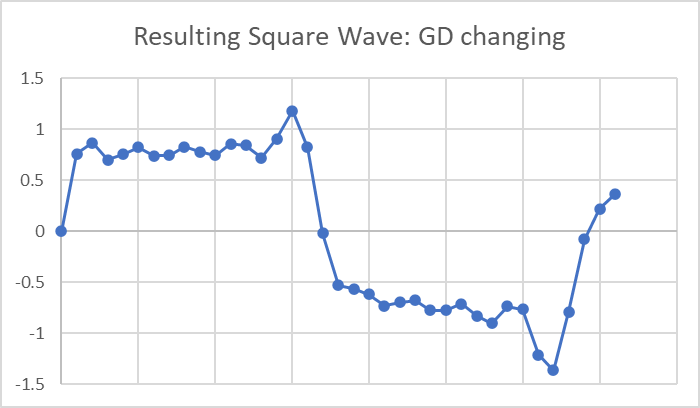
We can see the difference more clearly by showing them both on the same plot:
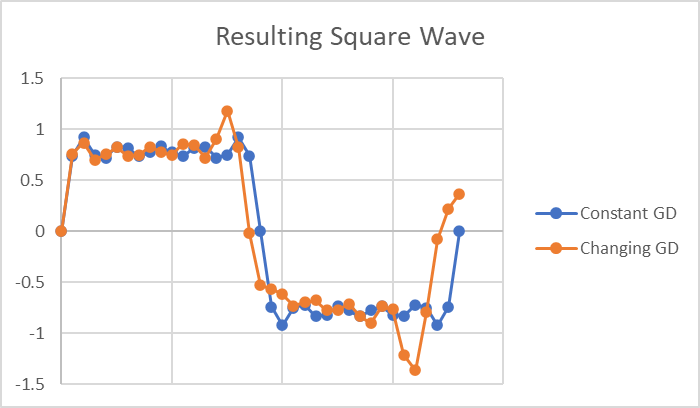
Hopefully this helps visualize how group delay can impact the signal, and why constant group delay is a typical design goal. - Don
A change in phase is equivalent to a time shift, for example a 180-degree phase shift is like shifting the time by one-half cycle of the signal. The derivative is a fancy expression for the slope of a line, so it is a measure of phase linearity. A straight (linear) line has the form y = mx+b where every point x is multiplied by the slope m and added to offset b to produce a y value. For a straight line, m is constant (just a number, not a function of something else), and hopefully we remember this formula from school. Now replace m with GD so to get a straight line, that means the change in phase divided by the change in frequency must be constant, meaning group delay is a constant, and every frequency is delayed by the same amount of time. What goes in, comes out again, exactly as it was but just a little later in time.
Now, a pulse, or musical signal, includes many frequencies. If we send the signal through a component like an amplifier or speaker with constant group delay, then every frequency is delayed the same amount, and the output is just like the input except delayed in time. If the group delay is not constant, that means different frequencies have different delays through the component, so at the other end the signal will be "smeared" in time with different frequencies arriving at different times. Things like transient attacks from drums or instruments will not be as clean. There are various studies discussing just how far off the delay can be at different frequencies before we notice it, some referenced in the Wikipedia article mentioned previously (https://en.wikipedia.org/wiki/Group_delay_and_phase_delay).
A straight line of y = mx with m = 1 looks like the blue line below. If I make the slope (m) depend upon the input (x) we get the orange line, which is no longer perfectly straight. The next plot shows the error. This is what happens when group delay is not constant, the (phase) line is no longer straight.
Now try with some signals, in this case the first five frequencies in a square wave. The amplitudes decrease as frequency goes up and only odd harmonics are used (see https://www.audiosciencereview.com/.../composition-of-a-square-wave-important.1921/). Notice how all nine signals line up in the middle and again at the end.
If all the signals arrive at the same time, that is group delay is constant, then this is what you see when you add them all up:
A perfect square wave has frequencies out to infinity, and this is just five, so it does not have perfectly sharp (straight) edges and the top and bottom are not perfectly flat. It is perfectly symmetric, however, with edges and top and bottom the same across the entire period.
Now adjust the group delay so it is not constant but instead each successively higher frequency is shifted just a little bit more. Notice how the signals no longer align perfectly in the middle and at the end but are spread out a bit:
The output when we sum them all looks different and is no longer symmetric:
We can see the difference more clearly by showing them both on the same plot:
Hopefully this helps visualize how group delay can impact the signal, and why constant group delay is a typical design goal. - Don
Last edited: