Amplifier Output Impedance (Damping Factor) and Speakers

[DonH56]

This is a reprint of an article written ca. 2011-2012. I've been meaning to rewrite and update it, but Life and Work keeps getting in the way, so I am reposting the original as-is. Take it for what it's worth, an introductory take on one of the potential causes for differences in sound among amplifiers driving different speakers.

There are two parts: an original, and a follow-on post with parameters tweaked to match some additional "real-world" amplifiers made after some readers questioned some of the results. The readers' comments are not mine to share but hopefully you won't miss them.

FYI - Don


Part 1

Showing the impact of speaker loading on amplifiers is not too hard but is tedious (at least it was for me!) I set up two amps and two speakers, then plotted the speaker impedance and frequency response at the amplifier terminals. The speakers were 8-ohm nominal, 3-way, with crossovers at 300 Hz and 3 kHz. The first amp is SS with 0.1 ohm output (damping factor of 80) rising to about 1 ohm (DF=12.5) at 20 kHz. This mimics the way a lot of amplifiers behave with rising output impedance with frequency. The second amp is a tube amp with 0.8-ohm output (DF=10) rising to about 4 ohms at 20 kHz (DF=2; this is about as bad as I have measured in the primordial past).

The top plot shows the impedance, the next the amplifier outputs, and in the bottom plot I repeated the first amplifier’s response and then showed differences from each other amplitude to that first (SS) amp.

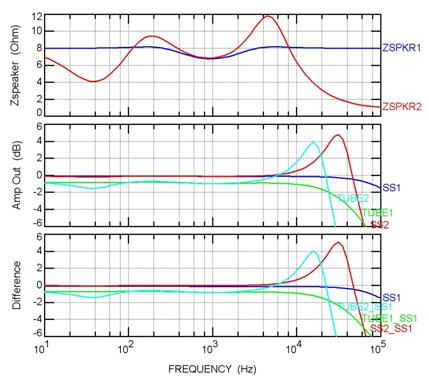
Speaker 1 shows pretty benign magnitude, with a slight dip where the midrange driver comes into play. The dip is because I used very simple first-order crossovers so there is some interaction among drivers. For the second speaker, I started with the network from the first, then added a roll-off at the high end to simulate a ribbon-type tweeter and a resonance dip to 4 ohms in the bass. This led to some peaks as well, though nothing terribly extreme.

Looking at the plots in the middle we can see how the amplifier’s impedances influence the response. A perfect amp would show a straight line. The SS amp into Speaker 1 (SS1, blue) shows very flat response with a bit of HF roll-off as expected. The tube amp into the first speaker (TUBE1, green) has a little less amplitude due to the higher impedance (this is insignificant since you’d just turn up the volume a little) and the HF roll-off kicks in sooner (again, expected for a tube amp). The plots into the second speaker are more interesting, with both amps showing some peaking at HF. This is because the rising output impedance is interacting with the capacitive load and causing a peak. Yes, this can happen in real life; it is one reason some amps are not stable with highly-capacitive loads. The peak is larger and at higher frequency with the SS amp (SS2, red) compared to the tube amp (TUBE2, light blue). This is because of the tube amps higher output impedance and faster HF roll-off. Note the tube amp into speaker 2 also has a LF dip, demonstrating the trouble it has driving low-impedance loads even at LF.

The final plot shows the SS amp into speaker 1, SS1 (blue), and the difference between that response and the other outputs. This is what we might hear when comparing amplifiers. Into the second speaker, the SS amp (red) is almost 3 dB higher at 20 kHz, peaking at ~5 dB at ~25 kHz, then rolling off. There is only about 1 dB difference at 10 kHz, rapidly decreasing to zero (a perfect match) below that. The tube amp into speaker 1 rolls off a little sooner, but is only about 1 dB down at 20 kHz, a difference we are unlikely to hear. Into the second speaker, the tube amp’s HF peak is about 4 dB at 15 kHz, dropping on either side. There is also that dip of ~1 dB at 30 Hz.

Can you hear this? I don’t know, but in a careful side-by-side test you might. Real amplifier and speaker impedances are more complicated and so might fare better or worse in a test. However, at least it shows that bad things can happen to good amps when presented with the real world of speakers.

HTH - Don


Part 2

Here are a new set of plots to address some of the comments made earlier. The SS amp now has a LF damping factor (DF) of 200 (0.04 ohm output) dropping to 50 (0.16 ohms) at 20 kHz. The tube amp went the other way, with an output impedance of 4 ohms (DF = 2) rising to 6 ohms (DF = 1.33) at 20 kHz.

There are no changes to speaker 1, still a pretty tame 8-ohm load, or speaker 2, dipping to 4 ohms at 40 Hz and ~3 ohms at 20 kHz (with a few other peaks and valleys). I added another speaker (3) that dips all the way to 2 ohms at 40 Hz, a milder HF load (~5 ohms at 20 kHz), but adds a high-Q peak around 1.5 kHz that raises the impedance to about 22 ohms.

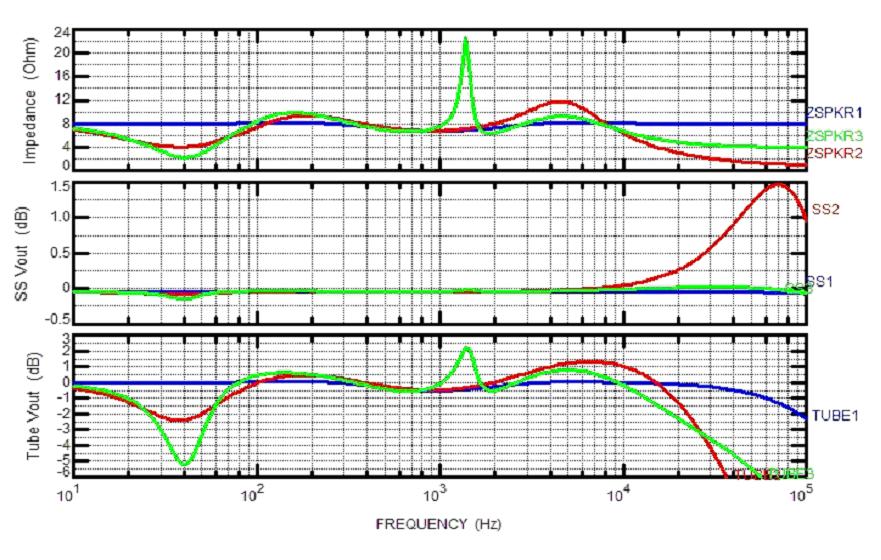
Now the SS amp performs pretty well into every speaker, though the low HF impedance of speaker 2 still reacts with the output inductance to peak 1.5 dB way up at 70 kHz (only ~0.25 dB at 20 kHz). The lower LF impedance dip of speaker 3 causes a very small dip, about 0.1 dB.

The tube amp struggles due to the much higher output impedance of the new model. It is OK with speaker 1 (have I mentioned how much I like my Magnepans?) but struggles with speaker 1 and 2.

This repeats work I did long ago, and no doubt done by many, many others. It helps explains my position on amps, which is that for most speakers I find it easy to distinguish a SS from a tube amp, find it almost impossible to pick from two SS amps at reasonable levels, and find it much harder to pick between two tube amps (though IME tube amps tend to vary much more than SS amps). This also helps explain why some people prefer certain amp/speaker pairings.

HTH - Don

 

[DonH56]

This is an update to the earlier posts describing how amplifier output impedance (or damping factor) might affect the sound you hear from your speakers.

First note damping factor, DF, is the load impedance divided by the amplifier’s output impedance: DF = Zload / Zamp. The load is usually the speaker’s impedance, plus that of the cables, and can be quite complex. The amplifier’s output impedance is also complex, though usually smoother than a speaker’s input impedance, and rises with frequency. This means an amplifier’s damping factor falls with frequency. Product data sheets, if they provide the damping factor at all, typically provide it for a simple 8-ohm resistor load at fairly low frequency like 20 or 100 Hz.

Second, while reasonably accurate from (fairly old) measured data, my amplifier and speaker models are still somewhat simplified without all of the detail a real-world amp and speaker might present. But I think they are good enough to show how amplifiers and speakers interact.

I have three amplifier models based upon published and measured data:

• AmpM is based upon a Marantz solid-state integrated amp. It is a good example of a fairly high-end design with wide bandwidth and generous feedback so the output impedance is very low and very flat over the audio band.
• AmpB is based upon a typical solid-state power amplifier (Benchmark) design.
• AmpA is based upon an ARC (Audio Research Corporation) tube amplifier design with transformer-coupled output and relatively low bandwidth and feedback.

There are four speaker models:

• Spkr1 is based upon a Magnepan planar-dynamic three-way design and is almost purely resistive.
• Spkr2 is a conventional ESL design with falling impedance at high frequency.
• Spkr3 is a hybrid ESL design representing a fairly complex load that sort-of combines the worst of dynamic and ESL characteristics.
• Spkr_st is the Stereophile speaker load pulled from their website.

The first simulation shows the output impedance and damping factor (DF) of each amplifier. Ignore the units on the DF plots; they are an artifact. AmpA has DF = 800 and is nearly flat over the audio band. AmpB starts around 200 and falls to about 50 at 20 kHz. AmpA has a DF of only around 2, falling slightly at 20 kHz.

Next the speaker load impedances are plotted (magnitude only). From top to bottom are the Stereophile speaker model, Spkr1 (Magnepan), Spkr2 (ESL), and Spkr3 (hybrid ESL). Spkr3, which I created many years ago (before I had the Stereophile model), is somewhat similar to the Stereophile load.

Now see what happens to the frequency response at the speaker terminals with each amplifier. Ideally, we would see a flat line independent of the speaker load. Deviation from a flat line indicates interaction between amplifier and speaker that can introduce frequency response variations from the speakers.

AmpM, at the top, exhibits almost no variation across the audio band with any speaker, with all excursions less than 0.05 dB. AmpB, in the middle, has some very high-frequency peaking driving Spkr2, but the deviation is only about +/-0.2 dB within the audio band. Note that the peaking is worse in this model than you are likely to observe with the actual amplifier. This level of deviation is probably inaudible (from either SS amp). AmpA, on the bottom, exhibits significant variations of several dB over the audio band with every speaker except the Magnepan (one reason tube amps work well with them).

The amplitude response variation due to amplifier output impedance (damping factor) is likely to be inaudible with either solid-state amp, but very noticeable with the tube amplifier (with the possible exception of the Maggies). Chances are, if you are comparing amplifiers, you would be able to readily discern the tube amplifier from the solid-state amplifiers, but if the only difference was output impedance you would be hard-pressed to differentiate between the two solid-state amplifiers. There are many other things that differentiate amplifiers, of course, including noise floor, power output, size, weight, heat, etc. but in my experience the amplifier’s output impedance and the speakers you drive can be a major contributor to sonic differences among amplifiers.

IME/IMO/FWIWFM/etc. - Don

 

[MrPeabody]

Don -

I haven't studied all these graphs in detail, but I sort of latched onto spkr2 and ampB because the behavior of spkr2 with ampB is so overtly different from the behavior of the other speakers with ampB. I looked at the impedance curves for ampB and spkr2. With all of the amps, the impedance rises at high audible frequency and continues to rise with increasing ultrasonic frequency. This suggests that for a speaker with a perfectly flat impedance curve, the speaker's share of the amplifier's true output voltage should decline starting at 10 kHz or somewhat earlier. Spkr2's impedance declines steadily above 5 kHz, and at face value it seems that this should compound the effect of the rising impedance of the amplifier. I.e., as frequency increases starting somewhat below 10 kHz, the speaker's share of the amplifier's true output voltage should steadily decline. But this is not what is indicated in your depiction of the effective frequency response of this spkr2 in combination with amplifierB. Either I'm misunderstanding something, or else it would seem that there is an error.

 

[DonH56]

Don -

I haven't studied all these graphs in detail, but I sort of latched onto spkr2 and ampB because the behavior of spkr2 with ampB is so overtly different from the behavior of the other speakers with ampB. I looked at the impedance curves for ampB and spkr2. With all of the amps, the impedance rises at high audible frequency and continues to rise with increasing ultrasonic frequency. This suggests that for a speaker with a perfectly flat impedance curve, the speaker's share of the amplifier's true output voltage should decline starting at 10 kHz or somewhat earlier. Spkr2's impedance declines steadily above 5 kHz, and at face value it seems that this should compound the effect of the rising impedance of the amplifier. I.e., as frequency increases starting somewhat below 10 kHz, the speaker's share of the amplifier's true output voltage should steadily decline. But this is not what is indicated in your depiction of the effective frequency response of this spkr2 in combination with amplifierB. Either I'm misunderstanding something, or else it would seem that there is an error.

Spkr2 is almost purely capacitive at HF and is interacting with the inductor modeling the rising output impedance of the amplifier, creating a resonant peak. A more complex model would hopefully not exhibit such a high peak. That said, in other (much earlier) amplifiers, such peaking due to the output choke led to instability and ultrasonic oscillations. So, while I do not believe a well-designed amp would have an issue with it, I have certainly seen (and repaired) amps that do...

 

[AdamG]

Amazing work @DonH56. Thread Sticked.

 

[Pdxwayne]

Hi Don,

For Part 1 in your first post, it seems plot 3 is a repeat of plot 2.

Can you do a simulation of a SS amp with damping factor of over 1K?

Thanks for the great work!

Oh, benchmark has an article that also factor in the speaker cables length and gauge. What is your assumption for speaker wires in your amp speaker calculation?

 

[Blumlein 88]

Could be titled: Why all amps don't sound the same with all speakers?

Good article.

 

[DonH56]

Hi Don,

For Part 1 in your first post, it seems plot 3 is a repeat of plot 2.

Can you do a simulation of a SS amp with damping factor of over 1K?

Thanks for the great work!

Oh, benchmark has an article that also factor in the speaker cables length and gauge. What is your assumption for speaker wires in your amp speaker calculation?

Forgot about that plot. Pretty much -- it is a difference plot but in that case the difference is the same as the plot above. I fixed it later, but the fix did not make it into the document I found. It was over ten years ago and I did not look closely.

The Marantz amp has DF = 800, pretty close to 1000, and very few amplifiers have lower output impedance. The variance is already <0.04 dB (40 mdB) at that point, so I'm disinclined to push it even lower. One of my frustrations is that it takes a few hours to put together a few plots and words around them, and I am lazy. Sorry. I tried to find a range of amps and speakers to model that was representative of the real world.

IIRC, the only amp I've had with DF~1000 was a Phase Linear 700, and that thing was unlovingly nicknamed a Blaze Linear for all the times it self-destructed.

There are no speaker wires. For reasonable gauges and lengths the difference is very small -- see the other thread where I simulated with and without speaker wire and saw essentially insignificant differences. https://www.audiosciencereview.com/...ffect-of-speaker-cable-length-mismatch.20150/ Speaker wires add to the driving impedance the speaker sees and thus will increase the deviation measured at the speaker terminals, but in practice the difference is very small for most home systems.

The idea behind this was to show that there are things that can audible cause differences among amplifiers, that are readily measurable, and are not related to amplifier distortion (which is usually so low as to be inaudible). I've had the idea for many years that output impedance (along with noise floor) accounted for some if not most of the audible differences among amplifiers. The genesis of these posts was mostly from an undergrad project around 1980, and that was several decades later than those who performed similar experiments before me.

I keep thinking of doing some sort of transient response but the real impact of that must include a better speaker model than I am using now. It needs to include a reasonable RLC (resistance, inductance, capacitance) model for back-EMF (charge kick-back) of the driver in an enclosure. I am not a speaker designer so don't have that sort of model at hand. I can do (I think) a decent model of the steady-state impedance from the frequency response but the dynamics of speaker operation I have not looked at since my grad school days. Peter Principle.

 

[Katji]

Could be titled: Why all amps don't sound the same with all speakers?

Good article.

Forum systems need smart bots like Reddit, then such posts and replies can automatically get bot replies with links to relevant reference posts.

 

[pogo]

I keep thinking of doing some sort of transient response but the real impact of that must include a better speaker model than I am using now. It needs to include a reasonable RLC (resistance, inductance, capacitance) model for back-EMF (charge kick-back) of the driver in an enclosure.

And this is where I see (and hear) the greater influence. For example, the swing-in and -out behavior can lead to a spongy reproduction in the low frequency range if the DF is too low. The amplitude differences are the smaller evil. The swing-in and -out behavior rather contributes to the sound reproduction. Besides, a more precise following woofer excites the room modes less.
I took the first step with the Purifis (DF > 800) and the second step with this and achieved an improvement each time:
I recently had a second pair of my speakers optimised by a tuner, replacing the mid-bass drivers with 'faster' ones. Result: My room modes are no longer excited so strongly that I was even able to deactivate my DSP correction in the range of 50-100Hz and I can hear more 'micro details'!

 

[MCH]

@DonH56 Hegel claims damping factors higher than 2000. What are your comments and what would you expect from that? Example:

H90

Manufacturer of hi-end audio electronics - amplifiers, preamplifiers, power amplifiers, D/A converters, CD-players and custom installation amplifiers.

www.hegel.com

 

[solderdude]

I assume more than 2000 in 8 ohm at 1kHz = 4mohm.
Add a cable to it and it drops down a lot.
Power a speaker with a woofer and passive XO in it and the DF at the woofer (which is what it is all about) is reduced to 100 or less.

High DF are a selling point that is moot.

Back in 1980 Kenwood had Sigma drive. Required 4-wire cable and feedback sensing was done at the actual speaker terminal (as well) as locally to lower the DF, which was popular back then, to numbers over 10.000.
This had other problems though and is utterly nonsensical.
It disappeared again quickly because it did not solve real problems. If it had every power amp would adopt this by now or something similar.

 

[pogo]

Hegel claims damping factors higher than 2000. What are your comments and what would you expect from that?

This question does not really arise and depends on the setup and taste.

With this high DF, you should be on the safe side for precise reproduction under all operating conditions.
A high DF is definitely decisive in my case. But this only works if the rest of the chain is potent enough (x-over, chassis, cables, contact resistors, ...). For speakers with deficits in the low frequency range, it can also be advantageous to work with smaller damping factors. This thickens the low frequency range, but has nothing to do with precise reproduction.
Some speakers don't like a lot of control, as their bass range benefits from a bass running on a "loose leash" (e.g. transmission line speakers).
Speakers with transformers (electrostats) often react unpredictably.

 

[LTig]

I assume more than 2000 in 8 ohm at 1kHz = 4mohm.
Add a cable to it and it drops down a lot.
Power a speaker with a woofer and passive XO in it and the DF at the woofer (which is what it is all about) is reduced to 100 or less.

High DF are a selling point that is moot.

Yep, because you have to add the DC resistance of the woofer to the cable to get the real damping factor of the woofer, and then it is much much lower. The only reason to have a low output impedance is to reduce the influence of the impedance curve of the speaker on the final frequency response of amp + cable + speaker.

 

[solderdude]

This question does not really arise and depends on the setup and taste.

With this high DF, you should be on the safe side for precise reproduction under all operating conditions.
A high DF is definitely decisive in my case. But this only works if the rest of the chain is potent enough (x-over, chassis, cables, contact resistors, ...). For speakers with deficits in the low frequency range, it can also be advantageous to work with smaller damping factors. This thickens the low frequency range, but has nothing to do with precise reproduction.
Some speakers don't like a lot of control, as their bass range benefits from a bass running on a "loose leash" (e.g. transmission line speakers).
Speakers with transformers (electrostats) often react unpredictably.

Alas there is no 'control' over the speaker and a low DF vs super low DF does not matter at all.
Here's why:

The speaker is a mechanical device. You apply a voltage and it takes time for the speaker to get to the point it is supposed to and at its resonance frequency it overshoots.
That overshoot generates a voltage (back EMF)
That is damped by mechanical damping (air, membrane etc) and the current through the coil.

Now here's the thing.
We have a woofer with a resonance at 40Hz. The impedance rises from say 8 to 40 ohm. Of course the actual resistance of the coil at such frequencies does not change. It is still 8 ohm.
The voltage applied (let's make this 8V for easy calculations).
For 1kHz the current drawn is 1A... 8V/8ohm.
At 40Hz the current is much lower than 8 ohm because there is a virtual resistance of 40 ohm. So at 8V 0.2A is drawn from the amp.
Where did the 0.8A go ?
Well... that is the back EMF current.
The woofer (acting as a microphone of sorts) has a DC resistance of 8 ohm and produces a current of 0.8A.
It thus is a voltage source with a 8 ohm source resistance.

That current can only be drawn if the speaker is shorted.
This is where the output resistance of the amplifier plays a role.

A DF of 50 = 0.16ohm
A DF of 1000 = 0.008ohm

The damping current thus is determined by the total resistance and the generated back EMF voltage.
8 ohm source + amp R out = total resistance that determines the damping current (current is what damps the motion).

for DF of 50: back EMF/8.16 ohm is not very different from back EMF/8.008 ohm
The resistance thus is 1.8% higher and the damping current for the poor DF situation thus is only 1.8% lower (0.15dB).
That is not going to 'grip' the driver nor affect the actual damping current.

What it does do is voltage division.

Connect such a speaker to an amp with 0.16 ohm out. Let 0.8A flow through that resistance and you get 0.128V.
0.128V opposite 8V = -35dB would be the distortion when one measures at the amp output (= 1.8% distortion) where the amp circuit itself on a test bench in a resistive load is near perfect and has 0.0001% distortion. (-120dB)
The same for the amp with 0.008 ohm and 0.8A = 0.65mV (-83dB)

So with the same load the DF 1000 amp has the same damping current and measures at its output -83dB distortion 0.007%
with the same load the DF 50 amp has the same damping current (well a tiny bit smaller) and measures, at its output, -35dB distortion 1.8%
While the amp itself, on a test bench in a resistive load, measures 0.0001% distortion. (-120dB) and the actual signal the speaker is fed is actually that. It just appears to be less because measured distortion is just a voltage opposite the reference voltage (8V)

So that part is current division in output resistance (current x resistance = voltage)

Now there is also a voltage division towards the speaker (no wire resistance, no XO filter).
8V open clamp of the amp.
output R = 0.16 ohm (DF 50) so the voltage division at 1kHz (8 ohm, close to Rdc) is 8/8.16 = 0.98*8V = 7.84V
output R = 0.16 ohm (DF 50) so the voltage division at 40Hz (40 ohm) is 40/40.16 = 0.996*8V = 7.97V
This means the voltage at 40Hz is 0.14dB higher than the 1kHz amplitude.
Measurable yes, audible... at the border of it.

output R = 0.008 ohm (DF 1000) so the voltage division at 1kHz (8 ohm, close to Rdc) is 8/8.008 = 0.9990*8V = 7.992V
output R = 0.008 ohm (DF 1000) so the voltage division at 40Hz (40 ohm) is 40/40.008 = 0.9998*8V = 7.998V
This means the voltage at 40Hz is 0.007dB higher than the 1kHz amplitude so not audible.

Changes heard thus are not damping current related but voltage division related.

This means the voltage at 40Hz is 0.14dB higher than the 1kHz amplitude.

The exact same thing happens with headphone amps and headphones. It is why one should not measure distortion or headphone amps (with a > 0 ohm output R) with a headphone that has a substantial impedance peak. You are measuring amplifier + voltage division of the damping current as 'error voltage'.

in short: current is what damps. As long as the DF is not much worse than 10 (1/8th 'rule') the damping current is not much different.
As long as the DF is not much worse than 10, due to voltage division, the frequency response of headphones (even with an impedance hump) does not change too much (audibly)
DF is determined by the output resistance and load resistance.
When the load resistance rises the DF always increases. The higher the load impedance the less important the output resistance is.
The smaller the increase in impedance is at the resonance frequency the less important the output resistance is.

 

[Bob from Florida]

Alas there is no 'control' over the speaker and a low DF vs super low DF does not matter at all.
Here's why:

The speaker is a mechanical device. You apply a voltage and it takes time for the speaker to get to the point it is supposed to and at its resonance frequency it overshoots.
That overshoot generates a voltage (back EMF)
That is damped by mechanical damping (air, membrane etc) and the current through the coil.

Now here's the thing.
We have a woofer with a resonance at 40Hz. The impedance rises from say 8 to 40 ohm. Of course the actual resistance of the coil at such frequencies does not change. It is still 8 ohm.
The voltage applied (let's make this 8V for easy calculations).
For 1kHz the current drawn is 1A... 8V/8ohm.
At 40Hz the current is much lower than 8 ohm because there is a virtual resistance of 40 ohm. So at 8V 0.2A is drawn from the amp.
Where did the 0.8A go ?
Well... that is the back EMF current.
The woofer (acting as a microphone of sorts) has a DC resistance of 8 ohm and produces a current of 0.8A.
It thus is a voltage source with a 8 ohm source resistance.

That current can only be drawn if the speaker is shorted.
This is where the output resistance of the amplifier plays a role.

A DF of 50 = 0.16ohm
A DF of 1000 = 0.008ohm

The damping current thus is determined by the total resistance and the generated back EMF voltage.
8 ohm source + amp R out = total resistance that determines the damping current (current is what damps the motion).

for DF of 50: back EMF/8.16 ohm is not very different from back EMF/8.008 ohm
The resistance thus is 1.8% higher and the damping current for the poor DF situation thus is only 1.8% lower (0.15dB).
That is not going to 'grip' the driver nor affect the actual damping current.

What it does do is voltage division.

Connect such a speaker to an amp with 0.16 ohm out. Let 0.8A flow through that resistance and you get 0.128V.
0.128V opposite 8V = -35dB would be the distortion when one measures at the amp output (= 1.8% distortion) where the amp circuit itself on a test bench in a resistive load is near perfect and has 0.0001% distortion. (-120dB)
The same for the amp with 0.008 ohm and 0.8A = 0.65mV (-83dB)

So with the same load the DF 1000 amp has the same damping current and measures at its output -83dB distortion 0.007%
with the same load the DF 50 amp has the same damping current (well a tiny bit smaller) and measures, at its output, -35dB distortion 1.8%
While the amp itself, on a test bench in a resistive load, measures 0.0001% distortion. (-120dB) and the actual signal the speaker is fed is actually that. It just appears to be less because measured distortion is just a voltage opposite the reference voltage (8V)

So that part is current division in output resistance (current x resistance = voltage)

Now there is also a voltage division towards the speaker (no wire resistance, no XO filter).
8V open clamp of the amp.
output R = 0.16 ohm (DF 50) so the voltage division at 1kHz (8 ohm, close to Rdc) is 8/8.16 = 0.98*8V = 7.84V
output R = 0.16 ohm (DF 50) so the voltage division at 40Hz (40 ohm) is 40/40.16 = 0.996*8V = 7.97V
This means the voltage at 40Hz is 0.14dB higher than the 1kHz amplitude.
Measurable yes, audible... at the border of it.

output R = 0.008 ohm (DF 1000) so the voltage division at 1kHz (8 ohm, close to Rdc) is 8/8.008 = 0.9990*8V = 7.992V
output R = 0.008 ohm (DF 1000) so the voltage division at 40Hz (40 ohm) is 40/40.008 = 0.9998*8V = 7.998V
This means the voltage at 40Hz is 0.007dB higher than the 1kHz amplitude so not audible.

Changes heard thus are not damping current related but voltage division related.

This means the voltage at 40Hz is 0.14dB higher than the 1kHz amplitude.

The exact same thing happens with headphone amps and headphones. It is why one should not measure distortion or headphone amps (with a > 0 ohm output R) with a headphone that has a substantial impedance peak. You are measuring amplifier + voltage division of the damping current as 'error voltage'.

in short: current is what damps. As long as the DF is not much worse than 10 (1/8th 'rule') the damping current is not much different.
As long as the DF is not much worse than 10, due to voltage division, the frequency response of headphones (even with an impedance hump) does not change too much (audibly)
DF is determined by the output resistance and load resistance.
When the load resistance rises the DF always increases. The higher the load impedance the less important the output resistance is.
The smaller the increase in impedance is at the resonance frequency the less important the output resistance is.

Which explains why the Bottlehead OTL headphone amp amir tested worked so well with the HD600 headphones. High output impedance amp plays well with high impedance load. Low output impedance amp plays well with wider load variation. DF higher than 10 yields diminishing audible results - super high DF numbers for marketing purposes. Excellent illustration!

 

[pogo]

Alas there is no 'control' over the speaker and a low DF vs super low DF does not matter at all. Here's why:

This idealized approach is known, but does not correspond to the listening experiences of many users and the third axis (time axis) including the swing-out behavior comes too short. Therefore, it would be even more important to have a useful speaker simulation model as DonH56 stated (e.g. changes with frequency, temperature and power level). But also a useful amplifier simulation model would be important!
See also here:
Link

 

[solderdude]

The swing out behavior is perfectly explained. Also harmonics are easily explained with the same explanation.
For the listening experience I have a very unpopular explanation amongst the better listeners.
This can only be verified by controlled experiments in blind tests.

Yes, a good speaker simulation that does not generate is definitely preferred to evaluate amp behavior in more realistic circumstances.
The problem here is standardization and which speaker should be emulated (all speakers react differently).
Various members have suggested loads. What is needed is a challenging load that is accepted or becomes a standard including protocols.
I don't see that happening though.

 

[DonH56]

@DonH56 Hegel claims damping factors higher than 2000. What are your comments and what would you expect from that? Example:

H90

Manufacturer of hi-end audio electronics - amplifiers, preamplifiers, power amplifiers, D/A converters, CD-players and custom installation amplifiers.

www.hegel.com

Others e.g. @solderdude have already answered. As a design goal, having the lowest practical output impedance over the greatest possible frequency range seems like a great idea to me. In practice, audibility depends upon the speakers and wiring to the speaker. For example, 12 AWG copper is around 1.6 m-ohms/ft (note there is a fairly wide range of published values; this is for solid copper wire, just for reference). A ten-foot (~3 m) 12 AWG cable is thus about 0.0016 ohms/ft * 10 ft * 2 (two wires to connect to the speaker) so about 0.032 ohms. For an 8-ohm speaker that yields an effective damping factor of 8/0.032 = 250 even if the amplifier had infinite damping factor (0 output impedance). That is one argument for placing the amplifier very close to the speakers and using short speaker cables.

If you have an amplifier with a DF = 2000, then for 8 ohms that adds 8/2000 = 0.004 ohms, for a resulting driving point impedance seen by the speaker of 0.036 ohms and effective damping factor of 222. My simulations, and various studies (that I am under no obligation nor particularly interested in dredging up again), have shown broad frequency deviations of a dB or so can be picked in in a blind comparison but are not particularly noticeable except in such a side-by-side comparison. A damping factor of 100 or more results in well under 1 dB variation for most speaker.

Note low output impedance (or not), and thus high damping factor is often at least partly the result of other design choices. Higher feedback to provide lower distortion will also lower output impedance (and raise DF). Higher power requires additional and/or larger output devices and that lowers output impedance. Class A designs, or those heavily biased into class A, need more devices to handle the thermal load and large steady-state current so may have low output impedance (countered in some designs by lower feedback for marketing if not engineering reasons so could go either way). Higher bandwidth often leads to greater internal (open-loop) gain that with feedback leads to lower output impedance. And so forth.

Personally I like low output impedances, or high damping factors, but that is just one factor in choosing an amplifier. My previous Magnepans were fairly low in impedance, but also pretty flat over frequency, so a low-DF tube amplifier worked well with them. My current Revel speakers are a much more challenging load and require much lower output impedance to prevent frequency variations. And there is always the back-EMF argument for low impedance that I am less familiar with (mainly because I don't have a good feel for, nor good models of, the back-EMF generated by a range of speakers). While interaction among components prior to the amplifier is usually low to insignificant, the interaction among amplifier output impedance, speaker cable, and speaker impedance and behavior can be quite significant.

With my Maggies I hardly paid attention to DF. With other speakers, I would probably pass on an amplifier that had <100, all else equal (it never is). Looking at two amplifiers with DF 100 vs. 200 I might be slightly biased to the one with 200. Comparing 200 to 500, less bias toward higher damping, and 500 to 2000 damping factor would not be a concern for either amp unless I had extremely demanding speakers.

I generally do not comment much on what you might hear -- far too many variables and I've no desire to debate what folk might or might not hear, or think they hear.

This got long, and has a lot of opinion in it, sorry - Don

 

[Matias]

This article is also very interesting on output impedance and frequency response.

SUMMER MUSINGS: No... Not all amplifiers sound the same (but many do! ;-).

A blog for audiophiles about more objective topics. Measurements of audio gear. Reasonable, realistic, no snakeoil assessment of sound, and equipment.

archimago.blogspot.com