- Thread Starter
- #21
i cant agree with this, ever heared of upsampling? imagine having two datapoints one at 0% volume, the other at 100% volume, now imagine doubling sampling size and having a third datapoint with 50% in between the two first ones, thats why upsampling actually makes a difference to the better (tho its a simplificated way to explain it)
As far as I know it only makes a difference in file size and container being used, and I have to admit that I don't get your idea with those volume levels, maybe it would make more sense if you'd use 25% (instead of 0), 50% (as low), and 100% (as doubled), but it's still not a very good example in my opinion.
thats why high khz files exist, its not about hearing above 20khz but its about having more datapoints so fast volume changes are more fluid and therefore sound better
its jsut that 192 khz files are named that way because in "theory" they can hold data that reproduces 192khz (or half that because of two channels) with the datapoints in the file, for 44,1khz material it means more resolution in the datapoints
...it's not like that. Sample rate's frequency is not really related to the actual audible frequencies or volume changes (dynamics). Simplifying all this we could say that sample rate is a resolution of digitized sound, and bit depth is a resolution of each sample. They also shouldn't be limited by bit rate per second as it is with lossy compression encoders.
You may also want to read those articles:
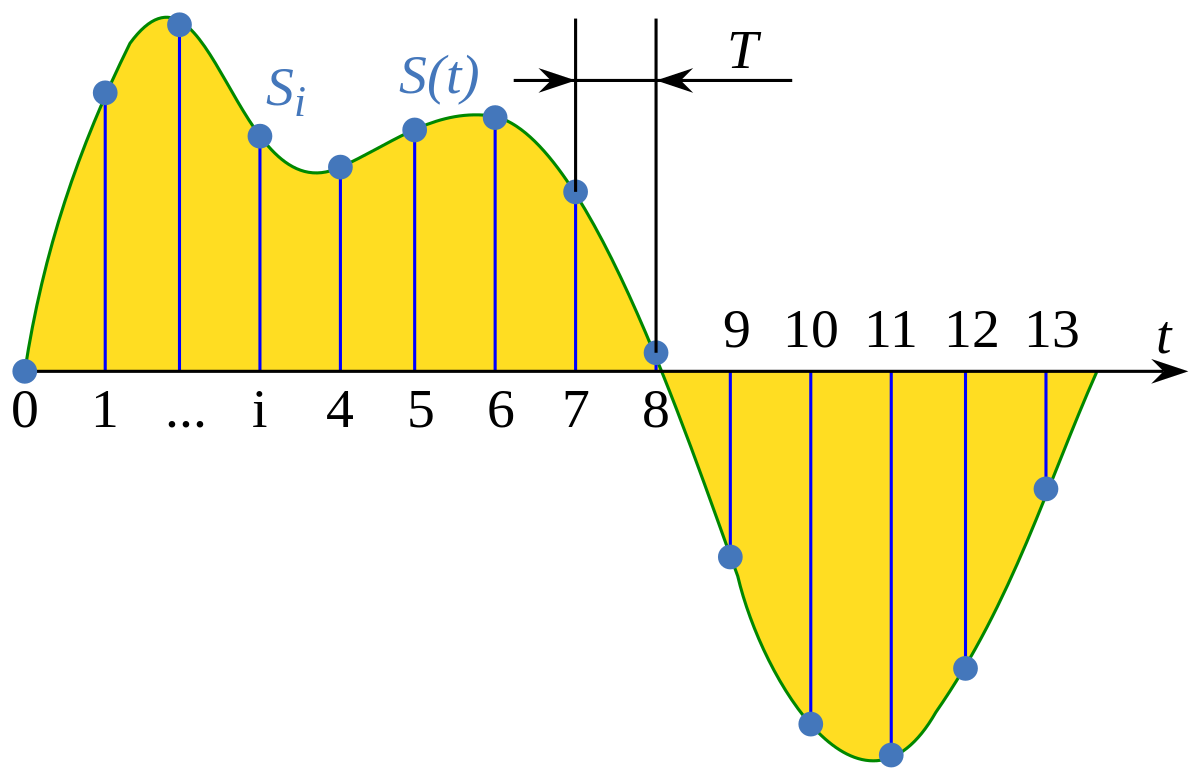
Sampling (signal processing) - Wikipedia
As a curio I can mention DSD (Direct Stream Digital) where only 1 Bit is used (instead of 16, or 24) with a very high sampling frequency.
Last edited:

